Linear Dynamical Systems
Let us start with an example. Consider the dynamics of an arbitrary linear thermal system. one typical case is a thermal field of semi-infinite soil. The x-coordinate axis takes the ground surface as its origin and measures depth underground. Underground heat propagates only by conduction, but convective heat transfer occurs on the ground surface, exposed to the external temperature. Also, radiation, evaporative cooling, and incoming solar radiation affect the surface. A discretization of space has been imposed, and thus the system is no longer continuous. The design featured, with thermal mass M, is affected by thermal conduction, convection, liberalized radiation, evaporative cooling, and solar radiation. Therefore, the temperature field is variable with time (t).
Social Viscosity; Reciprocity Mechanisms
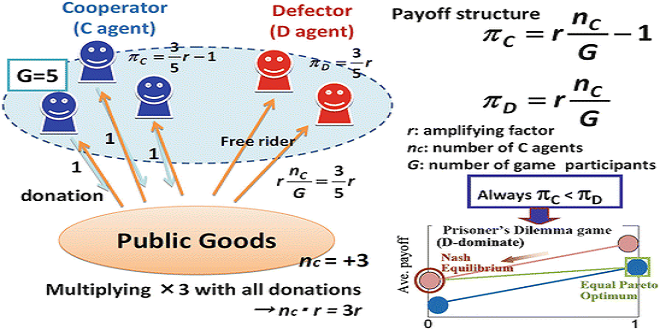
As long as an infinite and well-mixed population is assumed, the theory correctly predicts the dynamics of any symmetric 2-strategy game and its equilibrium, as we discussed in Sects.
Although the fundamental theory seems transparent and unsurprising, the interdisciplinary field around the study of evolutionary games has been persistent, with a new paper appearing every day or even every hour or minute. What has aroused this enthusiasm to study the field in mathematicians, biologists, physicists, formation scientists, and even ordinary foot soldiers such as the author? It comes down to a single question: What additional mechanisms will promote the ultimate cooperation among agents if a pair of agents are randomly selected from an unlimited group (i.e., an infinite and well-mixed selection) and forced into a specified game (such as PD)? In the natural world, cooperative behavior is found in human societies and among social insects such as ants and bees. This question invokes the mysteries of biological evolution and invites analogies with the statistical physics of crystal structure and phase transitions. Solutions may lead to suggestions for an improved human society.
Analytical Approach
Taylor and Nowak successfully deduced that any of the five reciprocity mechanisms by Nowak could be expressed by each transformation applied to an actual game payoff. This allows us to derive the equilibriums of each of the five mechanisms when using the replicator dynamics based on the transformed matrix.
In this sub-section, following the analytical approach presented by their work, we determine whether Dg 0 and Dr 0 are theoretically consistent as scaling parameters for evaluating each of the five reciprocity mechanisms. After confirming this theoretical consistency, we demonstrate that the set of these new scaling parameters works well in a finite and well-mixed population. Finally, we show that Dg 0 and Dr 0 can prove that the “paradox of cooperation” reported by Ne ´meth and takas is no paradox at all.
Theoretical Consistency for Nowak’s Five Reciprocity Mechanisms
Following Taylor and Nowak (2007), let us describe how Nowak’s five reciprocity mechanisms can be expressed by applying their respective transformed game matrices.
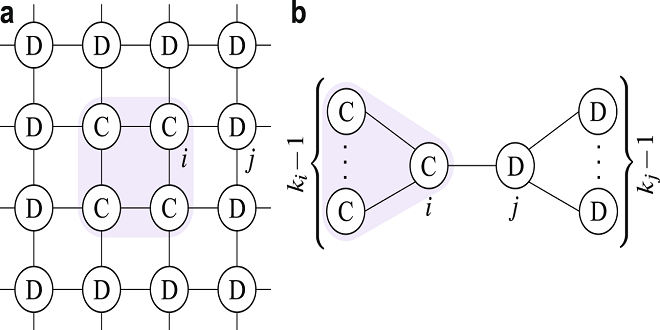
Theoretical Consistency for Finite Well-Mixed Population
Even a well-mixed population should be considered for the influence of social viscosity when the people in not infinite but finite. Although being a limited, well-mixed population is not one of Nowak’s five reciprocity mechanisms, “finiteness” allows the possibility of repeated encounters between two agents. Because of a finite population, we cannot apply replicator dynamics. We should discuss the so-called fixation probability in this situation, i.e., whether a selection favors the mutant’s strategy over the resident’s strategy.
Let us consider a Moran process with frequency-dependent fitness. At each round, an individual is chosen for reproduction proportional to its fitness. One identical offspring is produced that replaces another randomly selected individual. The fixation probability of C (D), ρC (ρD), is given by the likelihood that a single C (D) player in a population of N 1 D agents generates a lineage of C (D) that does not become extinct, but rather takes over the entire population.
Finally comment
Let us carefully observe the evolution. We can see the main remnant strategies on the equilibrium at the right margin of the graph. In contrast, the temporarily prosperous approach to the evolution process at the upper margin is enclosed by a break line rectangle. At the early stage of the evolution, strategies try to exploit others perish. At this moment, the final remnant plans are minorities, besides the temporarily successful strategies aiming at obtaining R at least. The remnants, however, gradually have grown over a quick process because they can get a higher payoff using CAD-type ST-reciprocity than R-reciprocity. Finally, they can overwhelm the temporary strategies.
